Overview
This article centers on mastering the standard deviation formula in Google Sheets, underscoring its critical role in data analysis and finance. It delineates the calculation process and clarifies the distinctions between the STDEV, STDEV.S, and STDEV.P functions. Furthermore, it offers a comprehensive step-by-step guide for employing these functions, accentuating their significance in making informed financial decisions driven by data variability.
Introduction
Understanding the variability within datasets is crucial for making informed decisions, particularly in finance, where data interpretation can significantly influence risk assessments and forecasts. This article explores the intricacies of standard deviation, a key statistical measure that quantifies how data points differ from the average. Yet, many professionals encounter difficulties in selecting the appropriate standard deviation formula in tools like Google Sheets and Excel, which can lead to potentially misleading analyses. How can one master these formulas to enhance data accuracy and decision-making?
Understand Standard Deviation and Its Importance in Data Analysis
Standard variation stands as a pivotal statistical measure, quantifying the variability or dispersion within a dataset. It elucidates how data points diverge from the mean (average). A low variation indicates that values cluster closely around the mean, while a high variation signifies a broader distribution of values. This understanding is particularly vital in finance, where variability plays a significant role in risk evaluation and financial forecasting.
For instance, in investment evaluation, a larger variance often correlates with heightened volatility, suggesting increased risk and potential return. Recent studies indicate that financial analysts increasingly rely on variability to gauge the stability of investment portfolios and economic indicators, underscoring its importance in informed decision-making. A greater variability in financial instruments can imply increased price fluctuation, frequently associated with higher investment risk.
Practical applications of variability measurement in finance encompass assessing the risk of stocks and investment strategies. Grasping the fluctuations of returns can substantially impact prediction accuracy. Furthermore, the variation measure is instrumental in evaluating economic indicators, aiding analysts in understanding trends and formulating forecasts.
Understanding and analysts, enhancing their ability to analyze data effectively and make strategic decisions based on numerical insights. As Charles Babbage aptly stated, 'Good quality information is the holy grail, and that’s what you should always strive for.'
Calculating standard deviation using the standard deviation excel formula involves:
- Determining the average
- Assessing deviations from the average
- Squaring those deviations
- Summing the squares
- Taking the square root of the variance
This process is essential for effective data analysis.
Explore STDEV, STDEV.S, and STDEV.P Functions in Excel
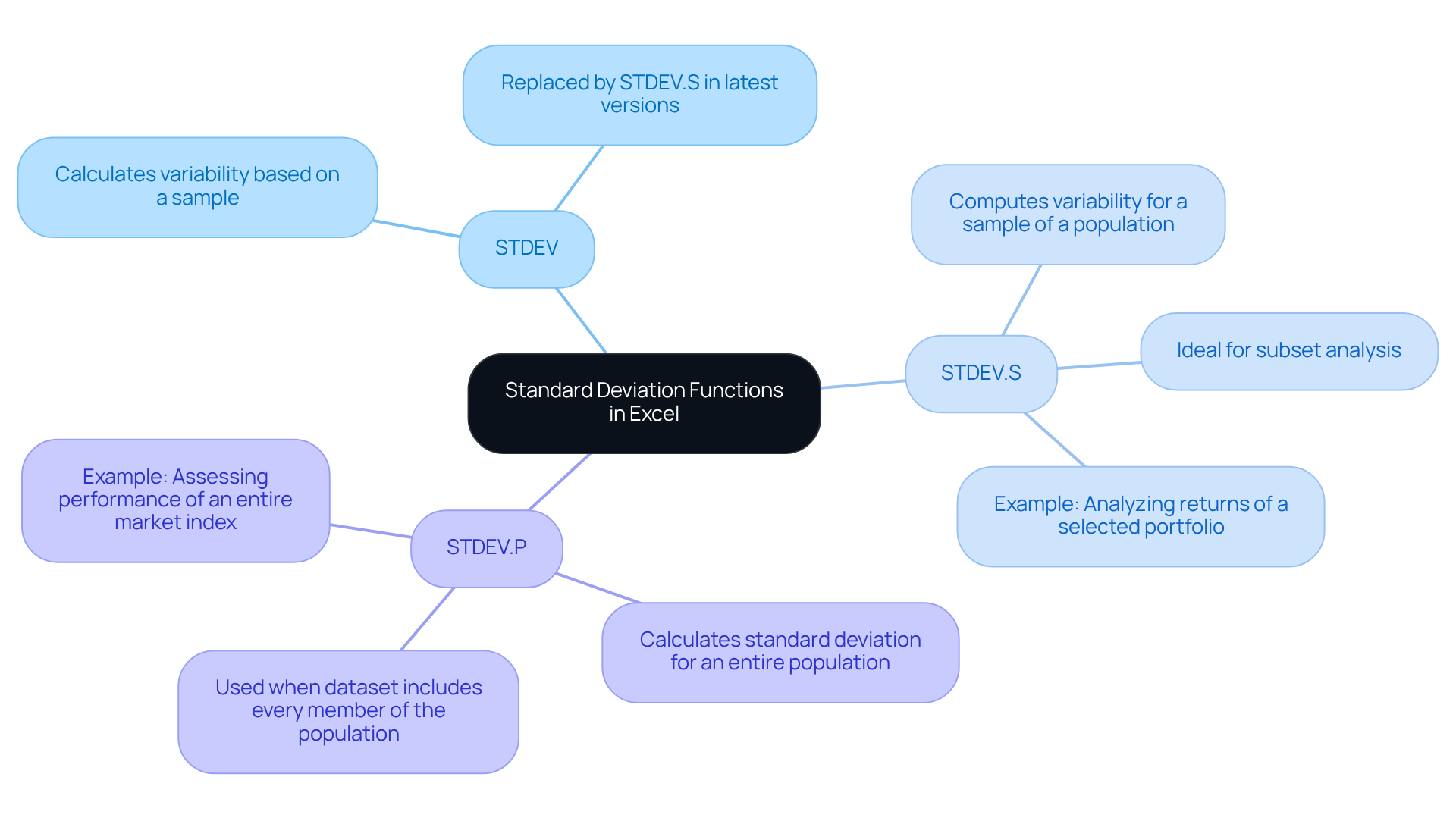
In Excel, the standard deviation excel formula consists of three primary operations used for calculating variability: STDEV, STDEV.S, and STDEV.P.
- STDEV: This operation calculates variability based on a sample but has been replaced by STDEV.S in the latest versions of Excel.
- STDEV.S: This method computes variability for a sample of a population. It is ideal when your data represents a subset of a larger population, ensuring your analysis accurately reflects the variability within that sample.
- STDEV.P: This operation calculates the standard deviation for an entire population. It should be employed when your dataset includes every member of the population being analyzed, providing a comprehensive view of variability.
Selecting the appropriate operation is essential for precise analysis; using the incorrect standard deviation excel formula can lead to misleading results. For instance, in financial analysis, choosing STDEV.S when only a sample is available can distort risk assessments, while applying STDEV.P on a sample may underestimate variability. As Hilary Mason articulates, "At the core of data analytics and data science is curiosity and learning; finding patterns, telling stories, and deepening your understanding of the world around you." This mindset is critical when determining which operation to utilize.
In practical terms, STDEV.S may be employed when analyzing the returns of a selected portfolio of stocks, whereas STDEV.P could be applied when assessing the performance of an entire market index. Understanding these distinctions not only enhances analytical precision but also supports in financial contexts.
Apply Standard Deviation Functions: A Step-by-Step Guide
To apply standard deviation functions in Google Sheets, follow these essential steps:
- Open Google Sheets: Access your Google Sheets document containing the relevant data.
- Select a Cell: Click on the cell where you wish to display the standard deviation result.
- Enter the Function: Input
=STDEV.S(range)for a sample or=STDEV.P(range)for the entire population. Be sure to replacerangewith the actual range of your data (e.g., A1:A10). Google Sheets offers this built-in formula, facilitating straightforward statistical calculations. - Press Enter: After entering the function, hit Enter. The cell will display the computed variation.
- Review the Outcome: Verify the result to ensure it meets your expectations based on the dataset.
By adhering to these steps, you can accurately compute the typical variation in Google Sheets using the standard deviation excel formula, leveraging your existing knowledge from Excel. Understanding this variation is crucial for finance professionals, as it assists in within datasets. A low standard deviation indicates that data points are closely clustered around the mean, while a high standard deviation signifies greater variability—an essential consideration for risk assessments and financial forecasting. If you find yourself overwhelmed by the numbers, take a moment to pause and regroup. Remember, mastering spreadsheets is a vital skill in today's data-driven landscape.

Conclusion
Mastering the standard deviation formula in Google Sheets is essential for anyone engaged in data analysis, especially in the finance sector. This statistical measure quantifies variability within a dataset and serves as a vital tool for informed decision-making. By accurately calculating standard deviation, analysts can assess risks, forecast trends, and interpret data with enhanced precision.
This article underscores the significance of standard deviation in data analysis, particularly in financial contexts where understanding volatility is paramount. It introduces the various functions available in Google Sheets—STDEV, STDEV.S, and STDEV.P—clarifying their specific applications and emphasizing the importance of selecting the appropriate formula based on the dataset. Additionally, a step-by-step guide is provided to streamline the calculation process, ensuring users can confidently apply these concepts in their analyses.
In today's data-driven landscape, the ability to interpret variability through standard deviation is invaluable. By leveraging these formulas, professionals can refine their analytical skills, facilitating more effective risk assessments and strategic decision-making. Seize the opportunity to deepen your understanding of standard deviation and utilize it to uncover insights that can significantly influence your financial analyses and beyond.
Frequently Asked Questions
What is standard deviation and why is it important in data analysis?
Standard deviation is a statistical measure that quantifies the variability or dispersion within a dataset. It helps to understand how data points differ from the mean (average). It is important in data analysis as it indicates the degree of spread in data, which is crucial for evaluating risk and making informed decisions, particularly in finance.
How does standard deviation relate to risk in finance?
In finance, a larger standard deviation often correlates with increased volatility, suggesting heightened risk and potential return. Financial analysts use variability to assess the stability of investment portfolios and economic indicators, making it a key factor in risk evaluation.
What are some practical applications of standard deviation in finance?
Standard deviation is used to assess the risk of stocks and investment strategies, helping analysts understand the fluctuations of returns. It also plays a role in evaluating economic indicators, aiding in the analysis of trends and the formulation of forecasts.
What steps are involved in calculating standard deviation using Excel?
The steps to calculate standard deviation using Excel include: 1. Determining the average of the dataset. 2. Assessing the deviations of each data point from the average. 3. Squaring those deviations. 4. Summing the squared deviations. 5. Taking the square root of the variance.
Why is understanding standard deviation crucial for finance professionals and analysts?
Understanding standard deviation enhances the ability of finance professionals and analysts to analyze data effectively, allowing them to make strategic decisions based on numerical insights and improve prediction accuracy.

